
신호 무결성의 개념 정의: 디퍼렌셜 페어
글/MENTOR, A SIEMENS BUSINESS
디퍼렌셜 페어란 고속 체제를 설계할 때 흔히 쓰이는 보편적인 net 토폴로지이다. 이 글에서는 디퍼렌셜 페어가 무엇인지 정의를 내리고 HyperLynxⓇ 필드 솔버를 사용해 디퍼렌셜 페어와 단일 종단 net 사이의 필드 분포 추세를 알아보기 쉽게 그래픽으로 제시한다.
본문에서 확인할 수 있겠지만, 디퍼렌셜 페어는 두 가지 유형의 신호를 전달한다. 하나는 net 페어를 오드(odd) 모드로 구동할 때 가동되는 차동 신호이고, 다른 하나는 net 페어를 이븐(even) 모드로 구동할 때의 공통 신호이다. 공교롭게도 공통 신호는 대체로 디퍼렌셜 페어에서 나타난다. 이것은 여러 가지 원인에서 비롯되는 현상인데, 자세한 내용은 본문에서 다루고자 한다.
디퍼렌셜 페어를 종결하는 것은 단일 종단 신호를 종결하는 것만큼이나 중요한 일이다. 하지만 디퍼렌셜 페어 쪽이 좀 더 문제가 복잡한데, 목표가 공통 신호와 차동 신호를 둘 모두 종결하는 데 있기 때문이다.
마지막으로 두 개의 디퍼렌셜 페어 사이의 누화에 관해 알아보자. net을 긴밀하게 커플링된 계획에 따라 라우팅하느냐 헐겁게 커플링된 계획을 따르느냐의 문제에 몇 가지 예시를 제시하여 명확한 답을 제시할 예정이다.
차동 신호와 공통 신호
디퍼렌셜 페어는 두 개의 전송 선으로 구성되어 있다. 전송 선은 긴밀하게 커플링될 수도, 헐겁게 커플링될 수도 있으며, 둘 사이에 커플링이 전혀 없는 경우도 가능하다. 디퍼렌셜 페어는 공통 신호와 차동 신호를 둘 다 전송할 수 있다.
차동 신호란 디퍼렌셜 드라이버의 양의 핀과 음의 핀 전압 차이라고 보면 된다. 즉 Vdiff = Vp - Vn으로 표시할 수 있다. 반면 공통 신호는 양의 핀과 음의 핀 전압의 평균을 말한다. 즉 수식으로 나타내면 Vcomm = 0.5⁎(Vp + Vn)이다. 그 결과로 발생하는 신호를 예시로 나타낸 것이 그림 1이다. 공통 신호가 없는 경우, 차동 신호의 진폭이 단일 종단 신호의 두 배가 된다. 또한 공통 신호가 항상 DC 신호인 것은 아닙니다. 때로는 전환 작동이 생기기도 한다.
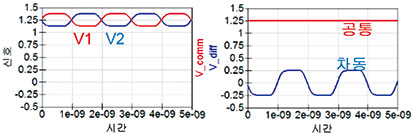
[그림 1] 차동 신호와 공통 신호
차동 신호는 한 쌍의 전송 선로를 통해 전달되기 때문에 각 트레이스의 오드(odd) 모드 임피던스의 두 배에 상당하는 차동 임피던스가 발생한다. 다시 말해 Zdiff = 2⁎Zodd이며, 여기서 Zodd가 선로 쌍(페어)을 오드(odd) 모드로 구동했을 때 각 전송 선의 임피던스이다. 한 쌍의 선로를 오드(odd) 모드로 구동한다는 말은 각 전송 선을 서로 반대 극성으로 구동한다는 말이다.
반면 공통 신호의 경우 이븐(even) 모드 임피던스의 절반에 상당하는 공통 임피던스가 발생하여 Zcomm = 0.5⁎Zeven이 되고, 여기서 Zeven이 선로 쌍을 이븐(even) 모드로 구동했을 때 각 전송 선의 임피던스이다. 전송 선 한 쌍을 이븐(even) 모드로 구동한다는 것은 두 회선을 모두 같은 극성과 진폭을 지닌 완전히 똑같은 신호로 구동한다는 뜻이다.
긴밀하게 커플링된 페어의 경우, 각 전송 선의 오드(odd) 모드 임피던스는 각 전송 선의 단일 종단 임피던스보다 진폭이 작아진다(Zodd < Z0). 반대로 이븐(even) 모드 임피던스는 각 전송 선의 단일 종단 임피던스보다 큰 임피던스를 가질 것이다(Zeven > Z0).
디퍼렌셜 페어가 언커플링되는 경우, Zodd = Zeven = Z0이 성립한다. 이것은 페어 사이에 커플링이 없기 때문이며, 구동 모드와는 관계없이 필드 패턴이 같고 임피던스에는 아무런 영향이 없기 때문이다.
디퍼렌셜 페어를 조사하려면 그림 2에 표시된 것과 같이 다음과 같은 두 가지 회로를 고려해야 한다. 위의 회로에서는 두 개의 동일한 드라이버(극성은 서로 반대)가 50Ω 레지스터로 종결된 두 개의 언커플링된 마이크로스트립을 구동한다. 각 마이크로스트립의 임피던스는 50Ω이다. 아래 회로의 경우 디퍼렌셜 드라이버 하나가 두 개의 긴밀하게 커플링된 마이크로스트립에 연결되어 있고, 이 마이크로스트립을 50Ω 레지스터로 종결하였다. 각 마이크로스트립의 오드(odd) 모드 임피던스 Zodd = 50Ω이다. 하지만 단일 종단 임피던스 Z0 = 57Ω이 성립한다. 위쪽 회로에서 두 개의 단일 종단 드라이버를 사용하는 것은 마이크로스트립에 공통 신호를 구동할 수 있도록 하기 위해서이다. 두 회로에 같은 드라이버 모델을 할당하였다.
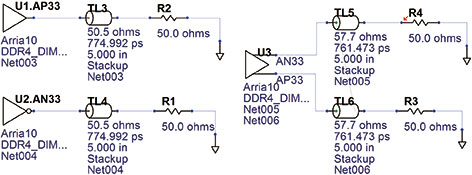
[그림 2] 드라이버 모델이 같은 디퍼렌셜 페어: 왼쪽이 언커플링된 마이크로스트립, 오른쪽이 긴밀하게 커플링된 마이크로스트립
우선, 디퍼렌셜 페어의 각 마이크로스트립에서 신호가 전달되는 방식을 살펴보면 유익한 정보를 얻을 수 있다. 이 시점에서 물을 만한 질문을 예로 들면 다음과 같다. 레지스터 R2와 R4에 도달하는 신호에 서로 차이점이 있을까?
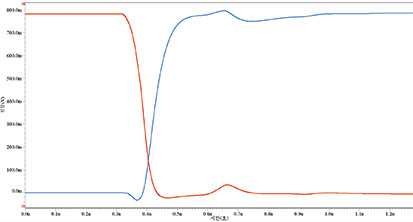
시뮬레이션을 실행하여 그림으로 나타낸 것이 그림 3이다. 맨 위의 그래프를 보면 R2의 언커플링된 회로에서 상승 에지가 측정되어 파란색으로 표시되었다. 빨간색 그림은 긴밀하게 커플링된 회로를 R4에서 측정한 것이다. 두 그림 모두 800mV의 같은 전압에서 안정된다.
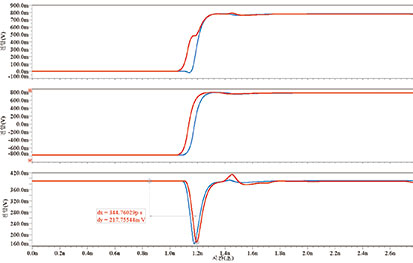
[그림 3] 커플링된 마이크로스트립과 언커플링된 마이크로스트립의 신호 비교: 맨 위의 그래프가 단일 선로, 가운데 그래프가 차동 신호이며 맨 아래 그래프가 공통 신호를 나타낸다. 파란색으로 표시된 것이 언커플링된 마이크로스트립을 통과하는 신호이며, 빨간색으로 표시된 것이 커플링된 마이크로스트립을 통과하는 신호이다.
R4의 긴밀하게 커플링된 회로에서 포착된 상승 에지의 작동 형태가 약간 다른 것을 볼 수 있다. 즉 빨간색 그래프에서는 500mV쯤 되는 지점에 정체 지점(shelf)이 있다. 이것은 두 트레이스 사이의 커플링 때문에 생긴 것이다. 이 회선은 마이크로스트립이기 때문에 특정 공명 주파수에서 종단 누화가 마치 High Q 필터와 같은 역할을 하여 신호의 전력을 일부분 흡수한다. 그림 3의 가운데 그래프는 각 회로의 두 레지스터에서 측정한 차동 신호를 나타낸 것이다. 두 회로 모두 길이가 같은 마이크로스트립에서 구동하였지만, 레지스터 R4와 R3의 차동 신호(빨간색 그림)는 파란색 그래프로 나타낸 레지스터 R2와 R1에서 측정한 것보다 최고 37ps 일찍 도착한다. 이것도 역시 커플링 때문이다.
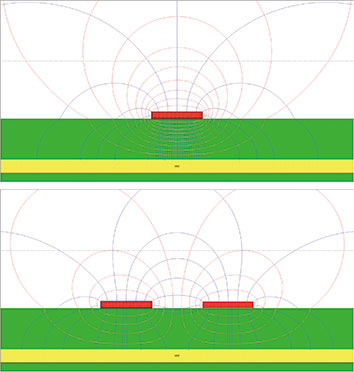
[그림 4] 필드 회선: 위는 오드(odd) 모드로 구동한 디퍼렌셜 페어, 아래는 단일 종단 회선
긴밀하게 커플링된 페어의 경우, 대부분의 필드 회선은 유전체가 아니라 공기 매개체에 존재한다.
따라서 속도가 단일 종단 회선에서보다 빠르다. 단일 종단 회선은 필드가 대체로 기판에 있다. 그림 4에서 이것을 알아보기 쉽게 나타냈다. 위의 그래프에서 파란색 E 필드 회선이 각 마이크로스트립에서 복사되며 공기를 통해 상대 회선으로 커플링된다. 하지만 아래 그래프는 단일 종단 회선을 나타낸 것인데, 여기서는 E 필드가 대부분 기판 안쪽에 있는 것을 볼 수 있다.
[그림 5] 상승 및 강하 파형의 비대칭
마지막으로, 그림 3의 맨 아래 그래프는 공통 신호를 나타낸 것이다. 대칭 채널에서 온전히 차동 신호만을 구동하는 대칭 모델이라고 가정한 상황인데, 비대칭은 어디서 발생한 것일까? 확인해 보니 상승 파형에 강하 파형에는 존재하지 않는 하락 구간이 있었다(그림 5 참조). 이 하락 구간 외에도 두 파형은 시간이 서로 어긋나며 400mV 쯤에 해당하는 가운데가 아니라 약 150mV 지점에서 서로 교차되었다. 그림으로 확인할 수 있듯이, 공통 신호는 양의 신호와 음의 신호 사이 평균인 400mV에서 시작한다. 신호가 전환되는 바로 그 지점에서, 공통 신호는 커플링된 마이크로스트립의 경우 217mV나 떨어진다(빨간색 그래프).
언커플링된 마이크로스트립도 마찬가지로 비슷한 폭으로 하락하기 때문에 하락 구간은 커플링 때문에 발생한 것이 아니라 모델 자체의 본질적인 특징 때문이라는 사실이 입증된다.
차동 신호와 공통 신호 종결
그림 6에 표시된 회로에서, 맨 위의 회로에서는 차동 신호와 공통 신호를 종결하는 데 똑같이 저항 T형 네트워크를 사용했다. 필드 솔버를 사용하여 각각의 회로에 사용된 서로 다른 임피던스를 계산한 결과는 다음과 같다. Z0 = 57.7Ω, Zodd = 49.6Ω 및 Zeven = 65.9 Ω이다.
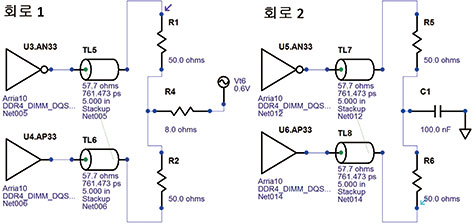
[그림 6] 종결된 디퍼렌셜 페어: 회로 1의 경우 풀업(pull up)을 포함한 레지스터 T형 네트워크를, 회로 2는 RC 종결을 사용
우선, 저항성 종결을 사용한 회로 1을 살펴보자. R1, R2 및 R4의 값을 추론하려면 전달 신호를 분석해야 한다. 차동 신호가 A와 B 노드에 도달하면 각 노드의 단일 종단 신호의 진폭은 같겠지만 상에서는 180° 벗어난 신호일 것이다. 이 두 개의 단일 종단 신호가 레지스터 R1과 R2를 통과한 다음 노드 C에서 서로를 무효화 해 버린다. 따라서 노드 C가 ‘가상’의 접지 역할을 하므로 차동 신호는 R1과 R2를 직렬로 접하게 된다. Zdiff = 2⁎ Zodd이므로, 결과 값은 R1 = R2 = Zodd = 49.6 또는 50Ω으로 도출된다.
공통 신호가 노드 A와 B에 도달할 때 서로 완전히 똑같은 단일 종단 신호의 형태를 띤다. 따라서 공통 신호에 관한 한 R1과 R2는 서로 병렬로 표시된다. 이는 즉, 지금까지 공통 신호에는 25Ω의 저항이 발생했다는 뜻이다. 다만 Zcomm = 0.5⁎Zeven = 33Ω이므로 25Ω의 저항을 33Ω까지 올리려면 아직 레지스터가 하나 더 필요한 상태이다. 다시 말해 R4가 8Ω이어야 한다. 이 결론을 계산하기 위한 공식은 R4 = 0.5⁎(Zeven - Zodd)이다. 여기서 전력 공급장치가 AC 신호 접지에 대한 매우 낮은 수준의 임피던스로 보이도록 설계했다는 점을 염두에 두시기 바란다. 이 때문에 Vt6 = 0.6V 풀업(pull-up) 전력 공급장치가 접지 단락과 같은 역할을 하는 것이다.
그림 6의 회로 2가 차동 신호에 대하여 이와 비슷하게 작동한다. 하지만 공통 신호의 경우 R4 레지스터를 커패시터로 대체하였다. R4를 제거한 이유는 긴밀하게 커플링한 전송 회선의 경우 레지스터 R4의 값이 매우 작아 무시할 수 있는 수준이기 때문이다. 헐겁게 커플링한 전송 회선 Zeven = Zodd이기 때문에 R4 = 0이다.
커패시터 C1은 전류에 DC 차단을 제공한다. 그렇지 않으면 대량의 전력 손실이라는 대가를 치러야 한다. 커패시터의 일반적인 값은 1~100nF 범위에서 다양하게 나타난다. 값을 선택할 때 RC 시간 상수가 최저 주파수 비트 패턴 기간보다 훨씬 길도록 선택해야 한다.
시뮬레이션을 두 번 실시하여 차동 신호와 공통 신호의 종결 상태를 테스트해보았다. 첫 번째 시뮬레이션에서는 각 회로의 드라이버를 서로 반대 극성으로 구동하여 순전히 차동 신호만 발생하게 하였다. 두 번째 시뮬레이션에서는 각 회로의 드라이버를 모두 같은 극성으로 구동하도록 설정하여 온전히 공통 신호만 발생시켰다. 그림 7은 그 결과를 그림으로 나타낸 것이다.
위의 그래프는 회로 1(빨강)과 회로 2(파랑) 사이의 차동 신호를 비교한 것이다. 두 파동 모두 잘 종결된 것을 알 수 있다. 아래 그래프의 공통 신호 또한 두 회로 모두 양호한 종결 상태를 보였다. 다만 회로 2(빨강) 파형 그래프에서 약 52mV 지점 쯤에 반사가 발생한 것이 눈에 보인다. 반사는 상승 에지가 도달하고 1.5ns 후에 수신기에 도달한다. 이것이 RX에서의 신호와 반대인데, 왜냐하면 이것은 드라이버의 저출력 공통 임피던스에서 반사된 것이기 때문이다. 여기서 마이크로스트립은 761ps이며 왕복 시간은 최대 1.5ns이다. 이 공통 신호 요소는 사소하고 반사된 것이기 때문에 중요하지 않다.
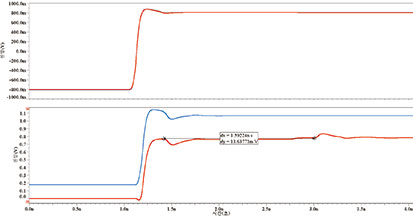
[그림 7] 위의 그래프가 차동 신호, 아래 그래프가 공통 신호. 파란색 그래프가 회로 1의 파형, 빨간색 그래프가 회로 2의 파형
긴밀한 커플링 대 헐거운 커플링의 채널간 누화 비교
긴밀하게 커플링된 디퍼렌셜 페어와 헐겁게 커플링한 것 사이에서 하나를 택해 결정해야 할 때, 대다수의 사람들은 긴밀하게 커플링된 페어를 쓰면 채널간(channel-to-channel) 누화가 적을 것이라고 생각한다.
귀환 평면이 없다면 이것이 사실일 수 있겠지만, 기판 레벨에서는 인접한 평면과의 커플링이 페어에 속한 트레이스 사이의 커플링보다 항상 크다. 이는 즉 평면에 대한 커플링이 디퍼렌셜 페어의 누화 여부를 좌우하는 지배적인 요인이라는 뜻이다. 트레이스가 긴밀하게 커플링되었는지 헐겁게 커플링되었는지에 상관없이 채널간 누화에 영향을 미치는 중요한 기준은 못 된다. 사실, 평면은 완전히 직감을 거스르는 형태로 작동한다. 이 예시를 보면 쉽게 확인할 수 있다.
그림 8에 표시한 세 개의 회로는 100Ω 디퍼렌셜 선로 페어를 구동한 것이다. 각 회로는 어그레서(aggressor) 디퍼렌셜 페어 채널 하나, 거기에 연결된 드라이버, 그리고 양쪽 종단에서 종결되는 빅팀(victim) 채널 하나로 구성된다. 회로도 내 모든 신호 회선은 5밀(1밀 = 1/1,000인치) 너비로 고정하였다. 종단간, 채널간 분리 또한 인접한 페어의 인접한 신호 회선 두 개 사이에서 5밀의 간격으로 고정하였다.
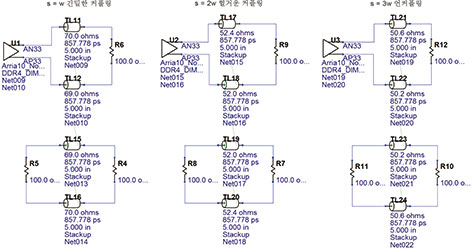
[그림 8] 긴밀한 커플링, 헐거운 커플링 및 언커플링 디퍼렌셜 채널의 채널간 누화 비교
각 페어의 p 회선과 n 회선 사이의 커플링은 세 가지 회로에서 각기 다르다. 긴밀하게 커플링된 회로의 경우 페어 내 두 회선 사이의 간격이 5밀이다. 헐거운 커플링의 경우, 각 페어의 회선 사이 분리 간격이 10밀이다. 언커플링된 회로의 경우, 각 페어의 회선 사이에 15밀의 간격을 두었다. 각 채널의 차동 임피던스를 모두 100Ω으로 똑같이 유지하기 위하여 분리 간격이 넓을수록 신호 회선과 참조 평면 사이의 거리는 줄였다.
상승 에지 시뮬레이션을 실시하여 NEXT (near-end crosstalk, 근단 누화) 채널에 대한 디퍼렌셜 채널을 알아냈다(그림 9 참조). 파란색으로 표시된 것이 ‘긴밀한 커플링’ 회로이며 녹색이 ‘헐거운 커플링’, 그리고 빨간색이 ‘언커플링’ 회로이다.
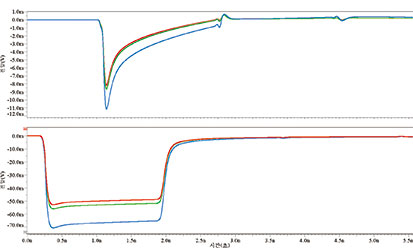
[그림 9] 맨 위 그래프가 FEXT, 아래 그래프가 NEXT. 파란색 선이 ‘긴밀한 커플링’, 녹색이 ‘헐거운 커플링’을 설명한 것이며 빨간색 그림이 ‘언커플링’ 회로
상승 에지가 발생했지만 NEXT에는 네거티브 피크가 나타났다. 이것은 빅팀 채널에 인접한 선로가 역방향 드라이버이고 이 때문에 하락 에지가 생기기 때문이다. NEXT를 나타내는 시그니처 파형은 펄스 폭이 넓은 것이며, 이는 세 가지 그림에서 모두 일치한다. 한 가지 주목해야 할 흥미로운 사실은 디퍼렌셜 채널간의 NEXT가 헐거운 커플링이나 언커플링 회로에서의 디퍼렌셜 채널간 NEXT에 비해 긴밀하게 커플링된 디퍼렌셜 페어에서 월등하게 크다는 점이다. 이것은 대다수의 엔지니어가 예상할 만한 것과 완전히 정반대의 결과이다. 긴밀하게 커플링된 디퍼렌셜 페어의 누화가 적은 것이 정상이 아닐까?
지오메트리를 살펴보면 명백한 답을 알 수 있다. 그림 10에서 보듯이 너비가 5밀인 선로에서 차동 임피던스를 100Ω 수준으로 유지하려면 각 디퍼렌셜 페어의 p 회선과 n 회선 사이 분리 간격이 넓을수록 유전체 두께를 줄여야 했다. 이는 즉 언커플링된 디퍼렌셜 페어를 포함한 회로의 경우가 세 가지 사례 중에서 귀환 평면이 신호 회선과 가장 가까웠다는 뜻이다. 누화를 줄이는 한 가지 방법으로 평면을 회선 가까이 가져와 필드가 인접한 선로가 아니라 평면에 더 많이 커플링되도록 하는 것이 있다. 바로 그 때문에 언커플링된 회로에서 NEXT가 가장 작고 긴밀하게 커플링된 회로에서 가장 큰 것이다.

[그림 10] 회로 스택업: 왼쪽이 긴밀한 커플링, 가운데가 헐거운 커플링이고 오른쪽이 언커플링된 회로
결론
이 글에서는 디퍼렌셜 페어에 대해 다루었다. 긴밀하게 커플링된 마이크로스트립에서의 차동 신호를 나타내어 언커플링된 마이크로스트립 페어에서의 차동 신호에서보다 약간 빠르게 신호를 전달한다는 사실을 제시하였다. 또한 저항 T형 네트워크와 RC 네트워크를 사용해 공통 신호와 차동 신호를 종결해 보았다. 마지막으로 이 글에서는 언커플링된 선로 페어가 긴밀하게 커플링한 선로에 비해 노이즈가 적다는 사실을 알 수 있었다.
추후 PCB 설계에서 신호 무결성 문제를 좀 더 잘 처리하고자 한다면, Mentor의 ‘신호 무결성의 개념 정의’ 시리즈를 검토해보기 바란다.
아날로그 설계를 위한 EDA 툴은 어떻게 진화하고 있는가?
조회수 795회 / Siemens EDA

전자제품 인터페이스의 설계 라이프사이클
조회수 595회 / David Wiens
전기 디자인 룰 체크(DRC)를 자동화하는 방법
조회수 1248회 /
 지멘스EDA 수석부사장.jpg)
2022년 시스템 및 설계 툴, 방법론의 시장 전망
조회수 1245회 / 지멘스
임계 영역을 이용한 자동차 IC의 테스트 품질 향상
조회수 1678회 / RON PRESS
SERDES 디자인을 위한 더 효율적인 솔루션이 있을까요?
조회수 1746회 / Neil Fernandes

지멘스 EDA 포럼 2021 열려, ‘Silicon to Systems’ 주제로 최신 설계 방...
조회수 1146회 / Joseph Sawicki
자동화된 EMC 분석을 PCB 레이아웃에 추가
조회수 1227회 / SIEMENS
DFT를 향한 성능 저하 없는 상향식 접근방식
조회수 2533회 / Geir Eide
PDF 다운로드
회원 정보 수정